डेसिबल ट्यूटोरियल: डीबी और डीबीएम बनाम गेन और मिलिवाट्स

एक डेसीबल (डीबी) की अवधारणा काफी मुश्किल है और किसी के लिए भ्रमित करने के लिए इसे पेश किया जा रहा है। लाभ, शक्ति और वोल्टेज (और वर्तमान, लेकिन ऐसा अक्सर नहीं) के लिए विशिष्टताओं को मिलाते हुए कि dB, dBm, dBW, वाट, मिलिवाट्स, वोल्टेज, मिलिवोल्ट्स, आदि को मिलाएं, अक्सर रैखिक मूल्यों और डेसीबल मानों के बीच आगे और पीछे परिवर्तित करने की आवश्यकता होती है। यह संक्षिप्त ट्यूटोरियल डेसिबल के साथ काम करने और रैखिक मूल्यों के साथ काम करने के बीच के अंतर को स्पष्ट करने में मदद करेगा।

लॉगरिथम (लॉग) को पहले स्कॉटिश गणितज्ञ जॉन नेपियर द्वारा शुरुआती एक्सएनयूएमएक्स में कल्पना की गई थी, क्रमशः गुणा और विभाजन के संचालन को सरल बनाने के लिए एक उपकरण के रूप में, उन्हें तेजी से और कम त्रुटि वाले जोड़ और घटाव संचालन में परिवर्तित करके। यह संभव हो पाया है क्योंकि जिस तरह से दो आधार संख्याओं को व्यक्त किया जाता है उसी तरह के आधार संख्या को घातांक के साथ केवल घातांक जोड़कर पूरा किया जा सकता है। उन समान संख्याओं का विभाजन घातांक घटाकर पूरा किया जाता है। यह घाघ के कानूनों में से एक है, और इस तरह दिखता है:

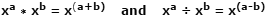
उदाहरण के रूप में वास्तविक संख्याओं का उपयोग करना, जहाँ x = 10, a = 4, b = 1:

एक्सप्लेंट्स का कानून किसी भी आधार संख्या के लिए काम करता है, न कि केवल एक्सएनयूएमएक्स। अर्थात:

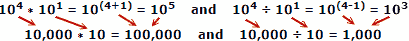
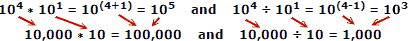
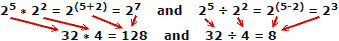
संख्याओं को जोड़ने और घटाने पर लोग कम गलतियाँ करते हैं, इसलिए लघुगणक का लाभ स्पष्ट है। याद रखें कि स्वचालित यांत्रिक या इलेक्ट्रॉनिक कंप्यूटर उपलब्ध होने से पहले लघुगणक विकसित किए गए थे। एक स्लाइड नियम गणना के लिए लघुगणक के गुणों का शोषण करता है, लेकिन यह एक अलग प्रमुख विषय है।

वे सरल उदाहरण हैं, लेकिन किसी भी आधार या प्रतिपादक के लिए हैं। कैलकुलेटर की अनुपस्थिति में, सामान्य अनुप्रयोग के लिए उपयोगी होने के लिए आपको संख्याओं की तालिका और उनके समतुल्य लघुगणक की आवश्यकता होती है। संख्याओं (1.000, 1.001, 1.002, 1.003, बनाम 1.0, 1.1, 1.2, 1.3, आदि) के बीच रिक्ति के आधार पर, प्रारंभिक लॉग टेबल भरे हुए वॉल्यूम। लघुगणक तालिकाओं के रचनाकारों के लिए अच्छी खबर यह है कि संख्या के केवल एक 'दशक' (उदाहरण के लिए, 1 के माध्यम से 10) की आवश्यकता होती है क्योंकि प्रत्येक पूर्ववर्ती या एकांत दशक XNXX की शक्ति का एक साधारण बहु है।

नोट: मैं इस चर्चा में आधार 10 का उपयोग करता हूं क्योंकि यह हमारी सामान्य संख्या प्रणाली का आधार है - इसलिए आधार 10 लॉग के लिए 'सामान्य लघुगणक' शब्द। आपने प्राकृतिक लघुगणक के बारे में सुना होगा, जो ई के आधार का उपयोग करता है, लेकिन स्केलर विद्युत शक्ति, वोल्टेज और वर्तमान मात्रा की गणना करते समय ई का उपयोग बहुत बार नहीं किया जाता है (हालांकि इसका उपयोग तब किया जाता है जब चरण कोण शामिल होते हैं, अर्थात, यूलर की पहचान)। प्राकृतिक लॉगरिदम को 'ई' सबस्क्रिप्ट के बिना ln (x) के रूप में लिखा जाता है, जबकि आमतौर पर बेस 10 लॉगरिदम को 10 सबस्क्रिप्ट के बिना लॉग (x) के रूप में लिखा जाता है; अर्थात्, क्रमशः loge (x) या log10 (x) नहीं।

प्रति बेस = 10 लॉग टेबल:

सेमी-लॉगरिदमिक 5 साइकिल इंजीनियरिंग ग्राफ पेपर - RF Cafe। अपवाद और विशेष मामला logx (0) = अपरिभाषित है। ऐसा इसलिए है क्योंकि कोई शक्ति नहीं है जिससे आप किसी भी संख्या को बढ़ा सकते हैं और 0 (शून्य) प्राप्त कर सकते हैं। आप असममित रूप से शून्य पर पहुंच सकते हैं, लेकिन आप शून्य पर नहीं पहुंच सकते। लॉग स्केल पर प्रदर्शित संख्या शून्य कभी नहीं होगी; वे आमतौर पर 10 की कुछ शक्ति से दस की किसी अन्य शक्ति से चलते हैं। लॉग ग्राफ पेपर का एक उदाहरण दाईं ओर दिखाया गया है। इसमें 5 'साइकिल' या 'दशकों' श्रेणी है। ध्यान दें कि y- अक्ष पर कोई शून्य नहीं है।

किसी संख्या का आधार- 10 (सामान्य) लघुगणक, तो वह घातांक है जिसे प्राप्त करने के लिए 10 को उठाया जाना चाहिए। दूसरे शब्दों में, चूंकि 10 की शक्ति 2 से बढ़ाई गई 100 (102 = 100) के बराबर है, 10 का आधार-100 2 (log10 100 = 2) है।

यह लघुगणक का मूल नियम है:


वास्तविक लघुगणक का उपयोग करके पृष्ठ के शीर्ष पर किए गए समान गुणा और भाग करना:



यह ठीक है, लेकिन आप जो चाहते हैं, वह उस संख्या का लघुगणक है जिसे आप चाहते हैं। प्रश्न: इस तरह एक सरल उदाहरण को छोड़कर, आपको उस उत्तर की आवश्यकता कैसे है? उत्तर: परिणाम के एंटीलोगरिथम (एंटीलॉग) को देखें। इस मामले में:

10 की पूर्णांक शक्तियां नहीं होने वाली संख्याओं के साथ एक कठिन और अधिक संभावित उदाहरण, निम्नलिखित कुछ जैसा लग सकता है:




 HP-35 कैलकुलेटर (विकिपीडिया) - RF Cafe 'x' के लॉगरिदम को 1.8444 के बराबर करता है, एंटीलॉग 'x' के बराबर होता है, जो 69.9 है



मैंने उन संख्याओं के लिए लॉग और एंटीलोग्स देखने के लिए अपने कैलकुलेटर का उपयोग किया, लेकिन 1972 से पहले जब Hewlett Packard (HP) ने अपने HP-35 वैज्ञानिक कैलकुलेटर को पेश किया, तो एक कॉर्पोरेट या विश्वविद्यालय के कंप्यूटर के एक्सेस के बिना औसत व्यक्ति को लॉग का उपयोग करने के लिए आवश्यक कंप्यूटर ऐसी गणना करने के लिए तालिका।

आज कौन आपको लघुगणक का उपयोग करने के लिए परेशान करता है, आप पूछ सकते हैं? बहुत से लोग, जिनमें मैं भी शामिल हैं, अक्सर जब शोर आंकड़ा (एनएफ) और अवरोधन बिंदु (आईपी) जैसे कैस्केड सिस्टम मापदंडों की गणना करते हैं। एनएफ और आईपी के साथ काम नहीं करते डीबी और पावर डीबीएम वैल्यू का सरल जोड़ और घटाव। शासी सूत्र, रैखिक लाभ और शक्ति मानों के गुणन और विभाजन का उपयोग करते हैं, जिसके लिए पहले डीबी और / या डीबीएम को रैखिक संख्या (लाभ अनुपात और mW) का उपयोग करना होता है, जो एंटीलॉग्स का उपयोग करते हैं, कैस्केड गणना करते हैं, और फिर परिणाम को dB और / में परिवर्तित करते हैं। या लॉग का उपयोग dBm।

सभी सिस्टम कैस्केड ऑपरेशंस को आगे और पीछे परिवर्तित करने की आवश्यकता नहीं होती है। उदाहरण के लिए यदि केवल कुल सिस्टम गेन और / या आउटपुट पावर लेवल की जरूरत है, तो गणना को रैखिक इकाइयों (mW और मल्टीप्लायरों) या लॉगरिदमिक इकाइयों (dBm और dB, क्रमशः) के साथ किया जा सकता है।

'DB' और 'dBm' की परिभाषा

इलेक्ट्रिकल इंजीनियरिंग में एक डेसिबल (डीबी) को एक्सएनयूएमएक्स के आधार के रूप में परिभाषित किया जाता है, जो दो पावर स्तरों के बीच के अनुपात के बेस-एक्सएनयूएमएक्स लॉगरिदम है; जैसे, पॉउट / पिन (दूसरे शब्दों में, लाभ)। अर्थात:

1 से अधिक सभी लाभ इसलिए सकारात्मक डेसिबल (> 0) के रूप में व्यक्त किए जाते हैं, और 1 से कम के लाभ को नकारात्मक डेसिबल (<0) के रूप में व्यक्त किया जाता है। ध्यान दें कि हम में से अधिकांश मामलों के लिए, P1 / P2 का रैखिक अनुपात एक धनात्मक संख्या (> 0) होना चाहिए क्योंकि 0 का लघुगणक अपरिभाषित है और ऋणात्मक संख्याओं का लघुगणक जटिल है (इनमें वास्तविक और काल्पनिक दोनों भाग होते हैं। )। डीबी मान, हालांकि, सैद्धांतिक रूप से + और + −∞ के बीच किसी भी मूल्य पर ले सकता है, जिसमें 0 भी शामिल है, जो 1 [10 * लॉग (1) = 0 डीबी] का लाभ है।

'dBm' एक डेसिबल-आधारित इकाई है जो 1 mW को संदर्भित है। चूँकि 0 dB ऑफ़ गेन 1 के लाभ के बराबर है, 1 mW की शक्ति 0 dB 1 mW, या 0 dBm से अधिक है। इसी तरह, dBW की एक पावर यूनिट 1 W के सापेक्ष डेसिबल है।


तदनुसार, 0 से अधिक सभी dBm मान 1 mW से बड़े हैं, और 0 से कम सभी dBm मान 1 mW (चित्र देखें। 1) से छोटे हैं। उदाहरण के लिए, + 3.01 dBm 3.01 dB 1 mW से अधिक है; अर्थात, या 0 dBm + 3.01 dB = + 3.01 dBm (2 mW)। −3.01 dBm 3.01 dW 1 mW से कम है; अर्थात, या 0 dBm + (N3.01) dB = N3.01 dBm (0.5 mW)।

निम्न तालिका कुछ संख्यात्मक उदाहरण देती है ताकि आप mW और dBm के बीच संबंध देख सकें। एक लघुगणकीय पैमाने पर दिए गए मूल्यों का एक ही सेट एक सीधी रेखा उत्पन्न करेगा। लॉगरिदमिक रिलेशनशिप के कारण ग्राफ लेफ्ट वर्टिकल ऐक्सस के मुकाबले छोटे वैल्यूज को बंच करता है। 0 से 1 mW क्षेत्र का एक आवर्धित संस्करण स्पष्टता के लिए इनसेट है।

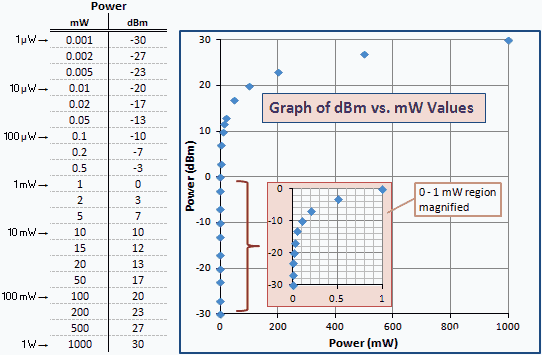
अंजीर। 1 - dBm बनाम mW की इकाइयों में बिजली का ग्राफ

अंजीर। 2 अंजीर में dBm बनाम डब्ल्यूडब्ल्यू के समान डीबी बनाम रैखिक लाभ अनुपात की एक तालिका और ग्राफ है। ध्यान दें कि संख्या और घटता बिल्कुल समान हैं; केवल अक्ष लेबल बदले जाते हैं। ऐसा इसलिए है क्योंकि dBm, 1 mW (1 dBm) के सापेक्ष dB में व्यक्त शक्ति की एक इकाई है।

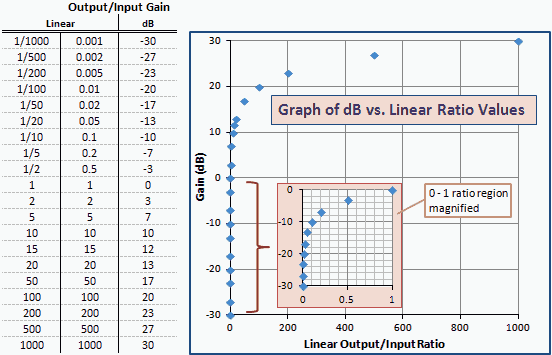
अंजीर। 2 - डीबीएम बनाम रैखिक अनुपात की इकाइयों में लाभ का ग्राफ

मौलिक रूप से, लाभ एक गुणन (या विभाजन) कारक है। एक उदाहरण के रूप में, एक एम्पलीफायर में एक लाभ हो सकता है जो इनपुट से आउटपुट तक 4 (यानी, 4x) के कारक से संकेत बढ़ाता है (चित्र देखें। 3)। यदि एक 1 mW (0 dBm) सिग्नल एम्पलीफायर में खिलाया जाता है, तो 1 mW * 4 = 4 mW सामने आता है। डेसिबल के संदर्भ में, 4 का एक कारक 10 * लॉग (4) = 6.02 dB के बराबर है, इसलिए आउटपुट पर 0 dBm के साथ-साथ 6.02 dBm का भी फायदा होता है + 6.02 dBm।

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

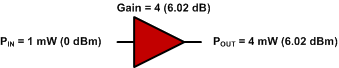
अंजीर। 3 - एकल एम्पलीफायर लाभ।

संयुक्त लाभ (रैखिक और dB) w / धनात्मक मान

यदि 4 के लाभ के साथ एक एम्पलीफायर 6 के लाभ के साथ दूसरे एम्पलीफायर के साथ श्रृंखला में है, तो कुल लाभ 4 * 6 = 24 है। डेसिबल के संदर्भ में, 6 का एक कारक 10 * log (6) = 7.78 dB के बराबर है, और 24 का एक कारक 10 * log (24) = 13.8 dB के बराबर है।

जैसे 4 x 6 = 24 (रैखिक लाभ), 6.02 dB + 7.78 dB = 13.8 dB (डेसीबल लाभ)।

यदि एक 1 mW सिग्नल (0 dBm) को एम्पलीफायर में खिलाया जाता है, तो 4 mW पहले एम्पलीफायर से बाहर आता है, और 24 mW दूसरे एम्पलीफायर से बाहर आता है। अंजीर देखें।

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

अंजीर। 4 - कैस्केड दोहरी एम्पलीफायर लाभ।

लाभ और हानि का संयोजन (रैखिक और डीबी)
यह अगला उदाहरण दिखाता है कि क्या होता है जब एक लाभ <1 (हानि) का सामना करना पड़ता है, जहां 1/6 के लाभ के साथ एक एटेन्यूएटर को दूसरे एम्पलीफायर के बजाय पहले एम्पलीफायर के बाद रखा जाता है। चित्र 5 देखें।
4 * 1 / 6 = 2 / 3 (रैखिक लाभ)। इसी तरह 6.02 dB - 7.78 dB = UM1.76 dB (डेसिबल गेन)।
पिछले उदाहरण के साथ, अगर 1 mW सिग्नल (0 dBm) को 4 के लाभ के साथ एम्पलीफायर में खिलाया जाता है, तो 4 mW निकलता है। यह 4 mW तब 1 / 6 के रैखिक लाभ के साथ एटेन्यूएटर में जाता है और 4 / 6 mW (2 / 3 mW) के शक्ति स्तर पर बाहर आता है।
इस मामले में कुल लाभ 4 / 6 = 2 / 3 है, इसलिए आउटपुट पावर वास्तव में इनपुट पावर से कम होगी।

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = X1.76 dBm

अंजीर। एक्सएनयूएमएक्स - कैस्केड एम्पलीफायर लाभ और एटेन्यूएटर।

12 mW + 34 mW + 8 mW + 20 dB

लघुगणक पर पूरक जानकारी
उत्पादों के लघुगणक
लॉगरिथम की एक संपत्ति का उपयोग उपरोक्त रूप से निम्नलिखित के रूप में किया जाता है, और उनके रैखिक समकक्षों को गुणा करने के बजाय लॉगरिदम मूल्यों को जोड़ने और घटाने में सक्षम होने का आधार है।

'h * j / k * m / n' उन घटकों के एक कैस्केड का प्रतिनिधित्व कर सकता है जिनके पास तीन डिवाइस हैं (h, j, और m) जिनमें से प्रत्येक का लाभ> 1 और दो उपकरणों (k और n) के साथ प्रत्येक <1 है (देखें) चित्र 6)। कुल प्रणाली लाभ की गणना या तो सभी रैखिक लाभ मूल्यों को एक साथ गुणा करके या सभी डेसीबल लाभ मूल्यों को एक साथ जोड़कर की जा सकती है।

अंजीर। 6 - कैस्केड घटक

महंगाई की मार
निम्नलिखित समझने के लिए महत्वपूर्ण है कि पावर के संदर्भ में पावर लाभ 10 * लॉग (Pout / पिन) dB क्यों है, जबकि वोल्टेज के संदर्भ में पावर लाभ 20 * लॉग (Vout / Vin) dB है।


ऐसा इसलिए है क्योंकि cf, c के गुणा के बराबर है जो कि 'f' बार है। उदाहरण के लिए, यदि f = 4:


वोल्टेज के आधार पर पावर बनाम पावर के आधार पर पावर गेन
पावर गेन पाउट / पिन है, और वोल्टेज लाभ वाउट / विन है। डेसिबल में पावर अनुपात के आधार पर पावर गेन को एक्सएनयूएमएक्स * लॉग (पाउट / पिन) के रूप में परिभाषित किया गया है। वोल्टेज के संदर्भ में पावर गेन, [(Vout10 / R) / (Vin2 / R)] है, क्योंकि ओम का नियम P = V2 / R है। हर में The R ’Vout2 / Vin2, जो कि (Vout / Vin) 2 के बराबर है, को रद्द करने के लिए रद्द कर दिया गया है, जैसा कि एक्स / bc = (a / b) c के घातांक के नियम द्वारा परिभाषित किया गया है। अत:

महत्वपूर्ण लेख: वोल्टेज के संदर्भ में वोल्टेज लाभ 10 * लॉग (वाउट / विन) डीबी है, शक्ति के संदर्भ में बिजली के लाभ के साथ ही। यह केवल तभी होता है जब वोल्टेज के संदर्भ में शक्ति लाभ व्यक्त किया जाता है कि 20 * लॉग (Vout / Vin) dB समीकरण लागू होता है। यह भ्रम की एक आम बात है।


गणित में कोई भी ऑपरेशन मनमाना नहीं है, और यह इस बात के लिए जाता है कि सिग्नल पावर लॉस (लाभ <1) को नकारात्मक मान के रूप में क्यों चित्रित किया गया है, और इसलिए इसे कैस्केड गणना के दौरान घटाया जाता है। यह एक साधारण प्रदर्शन है, लेकिन उल्लेख के योग्य है।

log (1 / f) = log (1) - लॉग (f) = 0 - log (f) = -log (f)

यदि आप एक रेडियो स्टेशन बनाना चाहते हैं, तो अपने एफएम रेडियो ट्रांसमीटर को बढ़ावा दें या किसी अन्य की आवश्यकता है एफएम उपकरण, बेझिझक हमसे संपर्क करें: [ईमेल संरक्षित].

एक संदेश छोड़ें 

संदेश सूची